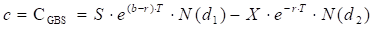
The generalized Black-Scholes model can be used to price European options on stocks without dividends [Black and Scholes (1973) model], stocks paying a continuous dividend yield [Merton (1973) model], options on futures [Black (1976) model], and currency options [Garman and Kohlhagen (1983) model].
TheoV
Call
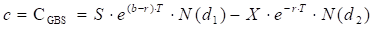
Put
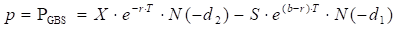
where
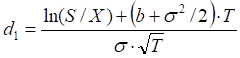
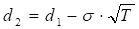
N(x) – the cumulative normal distribution function;
S – underlying price;
X – strike price of option;
r – risk-free interest rate;
T – time to expiration in years;
σ – volatility of the relative price change of the underlying stock price.
b – the cost-of-carry rate of holding the underlying security.
b = r gives the Black and Scholes (1973) stock option model.
b = r – q gives the Merton (1973) stock option model with continuous dividend yield q.
b = 0 gives the Black (1976) futures option model.
b = r – rf gives the Garman and Kohlhangen (1983) currency option model (rf - risk-free rate of the foreign currency).
Delta
Call
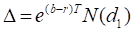
Put
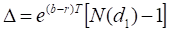
Gamma
Gamma is identical for put and call options.
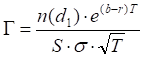
where
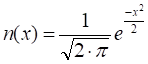 - normal
distribution function.
- normal
distribution function.
Vega
Vega is identical for put and call options.
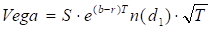
Theta
Call
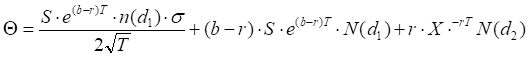
Put
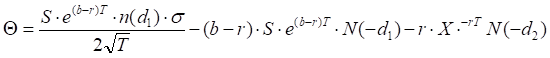
Rho
Call

where
c – call TheoV
Put
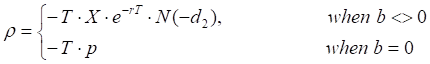
where
p – put TheoV
Implied volatility
To find implied volatility the following equations should be solved for the value of sigma:
Call
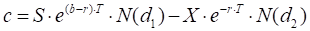
Put
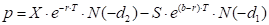
where
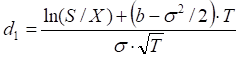

This equation has no closed form solution, which means the equation must be numerically solved to find σ.