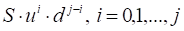
The Cox-Ross-Rubinstein binomial model can be used to price European and American options on stocks without dividends, stocks and stock indexes paying a continuous dividend yield, futures, and currency options.
TheoV
The main binomial model assumption is the underlying price can either increase by a fixed amount u with probability p, or decrease by a fixed amount d with probability 1-p. So the underlying price at each node is set equal to
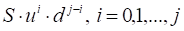
where
S – underlying price;
u, d – up and down jump sizes that underlying price can take at each time step.
Option pricing is done by working backwards, starting at the terminal date. Here we know all the possible values of the underlying price. For each of these, we calculate the payoffs from the derivative, and find what the set of possible derivative prices is one period before. Given these, we can find the option one period before this again, and so on. Working ones way down to the root of the tree, the option price is found as the derivative price in the first node.
Call
At expiration date:
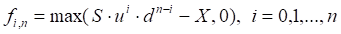
where n – number of time steps.
At each previous step:
European exercise
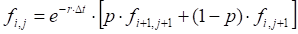
American exercise

where
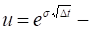 price up movement size;
price up movement size;
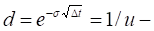 price down movement size;
price down movement size;
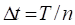 – size of each time step;
– size of each time step;
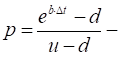 up movement probability;
up movement probability;
b – the cost-of-carry, defined as:
b = r to price European and American options on stocks;
b = r – q to price European and American options on stocks and stock indexes paying a continuous dividend yield q;
b = 0 to price European and American options on futures;
b = r – rf to price European and American currency options (rf – risk-free rate of the foreign currency).
Put
At expiration date:
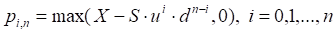
At each previous step:
European exercise
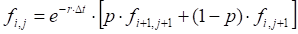
American exercise
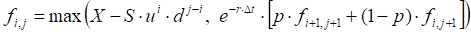
Delta
Given the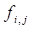 values calculated for the
price, Delta approximation is
values calculated for the
price, Delta approximation is
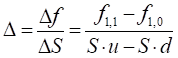
Gamma
Gamma approximation is
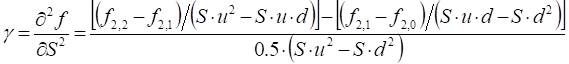
Theta
Theta can be approximated as
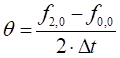
Vega, Rho
System uses the numerical differentiation to calculate the Greeks.
Implied volatility
System numerically finds implied volatility.