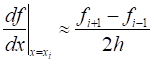
Abromowitz and Stegun approximation
The following approximation of the cumulative normal distribution function N(x) produces values to within six decimal places of the true value.
When x >= 0
N(x) = 1 – n(x)(a1 * k + a2 * k^2 + a3 * k^3 + a4 * k ^ 4 + a5 * k ^5)
when x < 0
N(x) = 1 – N(-x)
where
n(x) – normal distribution;
k = 1 / (1 + 0.2316419 * x);
a1 = 0.319381530;
a2 = -0.356563782;
a3 = 1.781477937;
a4 = -1.821255978;
a5 = 1.330274429;
Hart’s approximation
This algorithm uses high degree rational functions to obtain the approximation. This function is accurate to double precision (15 digits) throughout the real line.
Methods for solving equations
|
Method |
Description |
|
Bisection |
The bisection method is a simple iterative root-finding algorithm. The method convergence is linear, which is quite slow. On the positive side, the method is guaranteed to converge. |
|
Newton’s |
Newton's method, also called the Newton-Raphson method, is an iterative root-finding algorithm. The method convergence is usually quadratic, however it can encounter problems for function with local extremes. Newton's method requests that function is differentiable. |
|
Newton Safe |
Newton Safe method is an iterative root-finding algorithm, which combines the bisection and Newton’s methods. The method however if function has local extremes convergence can be linear. Like Newton's method, Newton safe method requests that function is differentiable. |
|
Brent’s |
Brent’s method is an iterative root-finding algorithm. This method is characterized by quadratic convergence in case of smooth functions and guaranteed linear convergence in case of non-smooth or sophisticated functions. |
The first derivative shall be calculated as
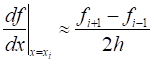
The first derivative represents instantaneous rate of change, which is limit of average rate of change where h is the small time interval,
h=the time between point t and point t+1=Δt (delta t)The second derivative shall be calculated as
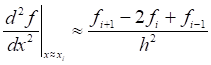
For further reading, we suggest:
•The Complete Guide to Option Pricing Formulas. ISBN 0071389970.
•Handbook of Mathematical Functions. ISBN 0486612724.
•Numerical Recipes: The Art of Scientific Computing. ISBN 0521880688.