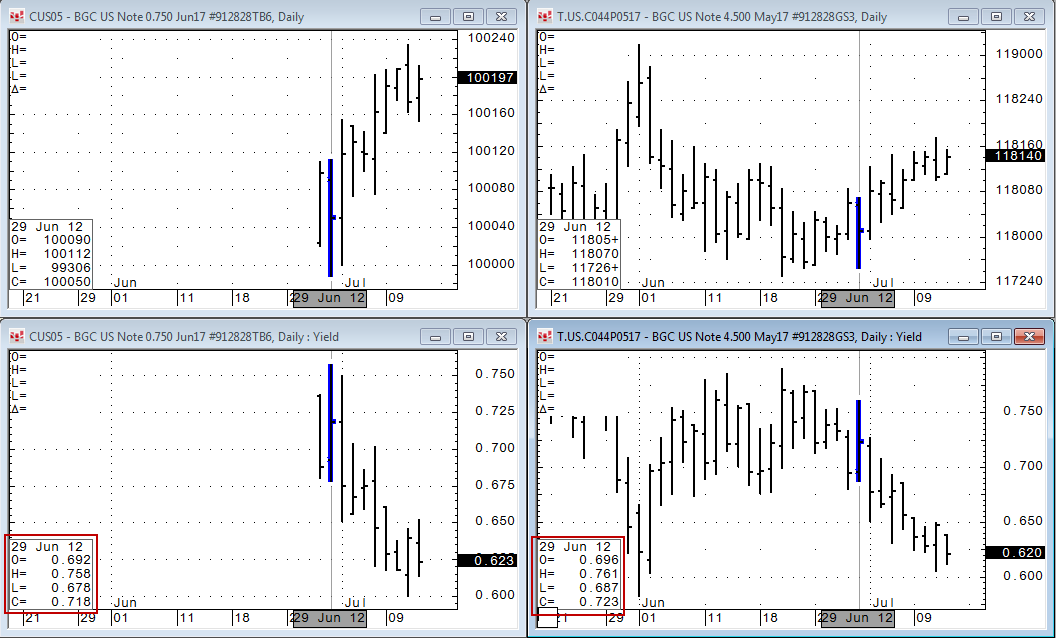
Yield charts plot the yield for debt instruments. These charts are used in the fixed income market.
This example considers a bar chart and a yield chart for two fixed income products.
The first product was just auctioned recently, so there is little historical data for use in forecasting. In this case, we can chart an existing product with a similar maturity date (May 2017 and June 2017) to simulate a chart of the more recent product.

Yield Parameters
|
Parameter |
Description |
|
Color |
Select color of bar. |
|
MarkIt |
Opens the Specify Conditions for Marking Bar window. |
|
Mode |
Choose from: Default = Calculates yield based on contract’s standard coupon and maturity. For example, TYA coupon is 6% and a 10-year maturity from today. Selecting Default for Yield(BTC10) uses the maturity, coupon, and price for the benchmark 10-year treasury. Specific Issue (only with futures) = Calculates yield of the futures contract based on the entered treasury maturity, coupon, and invoice price (futures price * conversion factor for that cash treasury). Custom = Calculates yield based on a treasury. For example, if you know the cheapest-to-deliver (CTD), then you can use that treasury’s maturity and coupon to calculate the futures contract yield. CME posts cheapest-to-deliver on their website under their Invoice Spread Calculator for each future tenor, so you don’t have to calculate it yourself. Using this mode, set the coupon rate and maturity date using the Contract data in the CME table. Eris = Calculates Eris futures contracts using Par Rate Equivalent. The handling of Eris contracts is described after this table. |
|
Calculation |
Opens sub-window with calculation parameters. The parameters listed depend on the mode selected: Specific Issue, Custom, or Eris. When underlying instrument is not a futures contract, then conversion factor and gross basis aren't used. Mode = Specific Issue Symbol = Type a treasury symbol (e.g. B033P1119) or its alias. You can also click the arrow button in that field to open the Specific Bond Issue window, where you can select a symbol from the list of returned values:
Convention = not editable Maturity = not editable Maturity Date = not editable CPN Rate = not editable CPN Freq = not editable Day Count = not editable Settlement = Delivery Date (future delivery date), Cash (uses Treasury Issue settlement convention), Custom (user-specified date) Settlement Date = only editable when Settlement = Custom Gross Basis = editable Mode = Custom This mode allows you to use a non-standard settlement date, such as delivery date, in the calculation. Convention = Choose Default, Standard Bill, Simple Bond, Moosmuller, Braess-Fangmeyer, Yield = 100 –price, or Yield = -price. Yield = 100 - Price, used for Eurodollar outrights Yield = - Price, used for native Eurodollar strategies and these groups of commodities: Calendar Spreads: EDAS1, EDAS2, EDAS3, EDAS Packs: EDAP1, EDAP2, EDAP3, EDAP4, EDAP5 Bundles: EDAB2, EDAB3, EDAB Butterflies, Double Butterflies, Condors: EDAL, EDAD, EDAC Maturity = Choose Default or Custom. If you select Custom, enter a maturity date. Maturity Date = Editable date when Maturity = Custom. CPN Rate = Select the rate. CPN Freq = Choose Annual or SemiAnnual. Day Count = Choose Actual/Actual, Actual/360, Actual/365, Actual/365-Japanese, Actual/365-ISDA, or 30/360 as a way to calculate accrued interested: Number of days in the coupon period/Number of days in the year. Settlement = Choose Default, Next Day, Second day, Third day, Fourth day, Fifth day, or Other. Settlement Date = Editable date when Settlement = Other. Gross Basis = editable Mode = Eris PV01 See details after this table. |
Related topics:
Eris Contracts and Par Rate Equivalent Yield
A Par Rate Equivalent yield model is available for Eris Futures contracts.
The model is calculated like this:
Par Rate Equivalent = NPV / PV01 / 10,000 + Contract Fixed Rate
where PV01 = ABS(FixedNPV / Coupon) * 10.0
Eris publishes the default PV01 value daily in their EOD settlement file. They provide this link to access the file: ftp://ftp.erisfutures.com/.
You can also use your own PV01 value.
The model can be applied to Yield charts and the Yield function in Formula Builder.
For more information about par rate equivalents, consult “ISV Guide for Calculating and Displaying Par Rate Equivalents” (May 2015) by Eris Exchange.
Calculating Mixed Eris and Non-Eris Strategies
For bonds with 182 days or less until maturity, the yield, using the Standard Bill model is calculated based on the following formula:
Yield = 100.0 *((d * Ay) / (Ad – (d * Tsm))
Where,
|
d = |
.01 * price (price in this case is the discount rate--the size of the price reduction for a 360-day period). |
|
Ad = |
Number of days in the year used for quoting discount securities (360). |
|
Ay = |
Number of days in a year for interest earned (365). |
|
Tsm = |
Days from settlement to maturity. |
For a bill with more than 182 days until maturity, the yield is calculated based on the following formula:
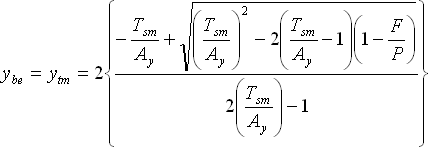
Where,
|
Ybe = |
Bond Equivalent Yield. |
|
Ytm = |
Yield to Maturity. |
|
Tsm = |
Days from settlement to maturity. |
|
Ay = |
Number of days in a year for interest earned (365). |
|
F = |
Face Value. |
|
P = |
Price. |
The concept of simple yield-to-maturity takes into account the drag to par which occurs if a bond is bought at either a premium or a discount and then held to maturity, at which time it is redeemed at par.
The simple yield on a bond uses the following formula:
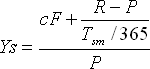
Where,
|
cF = |
Annual Coupon (in dollars). |
|
R = |
Redemptions Value. |
|
P = |
Clean Price of a bond, i.e. the price paid for the bond without any accrued interest. |
|
Tsm = |
Days from settlement to maturity. |
The standard bond formula is expressed as follows:
Where,
|
P = |
Price of the bond. |
|
v = |
The annuity variable. v = (1+Yw)^(-1) |
|
Yw = |
Yield to maturity divided by the number of coupons per year. |
|
tsn = |
Days from settlement date to the next coupon date. |
|
C = |
Coupon payment. |
|
N = |
Number of remaining coupon payments. |
|
R = |
Redemption value. |
|
AI = |
Accrued interest. |
|
Cn = |
Next coupon payment. |
If there is only one coupon left, the Standard bond model uses the same formula as the Moosmuller method.
The Moosmuller method, used by the U.S. treasury to determine the price of T-notes and T-bonds, given the yield, is exactly the same as the Standard model, except the Moosmuller method uses money market discounting from the next coupon date back to the settlement date. This difference is seen in the lead factor of the Moosmuller equation shown below:
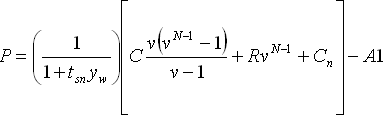
where
|
P = |
Price of the bond. |
|
tsn = |
Days from settlement date to the next coupon date. |
|
Yw = |
Yield to maturity divided by the number of coupons per year. |
|
C = |
Coupon payment. |
|
v = |
The annuity variable. v = (1+Yw)^(-1) |
|
N = |
Number of remaining coupon payments. |
|
R = |
Redemption value. |
|
Cn = |
Next coupon payment. |
|
AI = |
Accrued interest from the last coupon payment date to the settlement date (as measured by the appropriate day-count convention). |
The BraessFangmeyer method computes prices and yields on an annual basis. Therefore, coupon payments are annual; periodic yields are converted to annual yields before using, and the remaining time to maturity is measured in years.
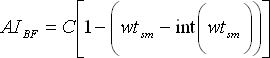
where
|
AI = |
Accrued interest from the last coupon payment date to the settlement date (as measured by the appropriate day-count convention). |
|
C = |
Coupon payment. |
|
w = |
Number of coupon periods per year. |
|
tsm = |
Days from settlement to maturity. |
|
Int = |
The annuity variable. Int = (1+Yw)^(-1) |