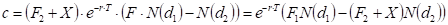Kirk’s Approximation

The approximation method by Kirk (1995) can be used to price European spread options on futures.

TheoV

Call price is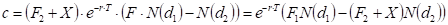
.

Put price is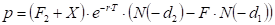
,

where
,

,

,

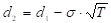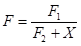and the volatility of F is approximated by the combined value:

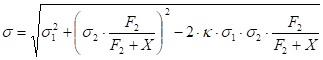
F₁ – price on futures contract 1,

F₂ – price on futures contract 2,

σ₁ – volatility of futures 1,

σ₂ – volatility of futures 2,

κ - correlation between the two futures contracts.

However, it should be noted that both formulas for andabove can be easily calculated using generalized Black-Scholes equation. Notice that if we take

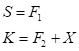
, and 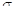is calculated by the formula above than 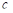may be expressed as

,

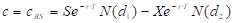which is exactly identical to BS equation. Similar is true for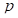. That also implies that some Greeks can be calculated by the corresponding BS formulas.

Prior to giving formulas for Greeks lets introduce a few helper equations which may help in implementing the formulas found across the section.

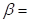
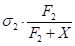
, thus simplifying.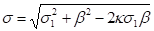

Put-call parity in Kirk’s model is expressed as:

.

Below are some partial derivatives used in equations

.

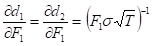The first derivative of sigma by the price of the second futures is:

.

The second derivative of sigma by the price of the second futures is a bit more complex and is:

.

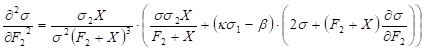Partial derivatives of 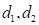by the price of the second futures are also useful to have. Those are:

,

.

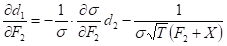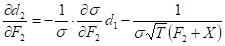Also, some partial derivatives of the combined volatility are as follow:

,

,

.

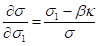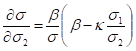Finally it should be noted that

,

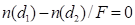and hence:

.

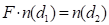Delta1, Delta2

Each delta is calculated with respect to the corresponding asset price movement. Sensitivity of call option price to price change of the first futures is:

.

Sensitivity of call option price to price change of the second futures is:

.

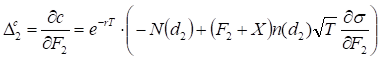By virtue of call-put parity given above the following expressions are true for put option Deltas. Sensitivities of put option price to price change in price of either the first or the second futures are, respectively:

,

.

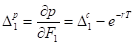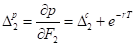Gamma1, Gamma2

Each gamma is calculated similar to delta, with respect to the corresponding asset price movement.

The equation is identical for call and put:

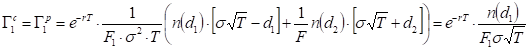
The gamma with respect to the second futures price is identical for call and put and is expressed as:

.

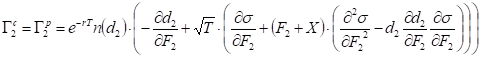Vega

The vega is chosen to reflect sensitivity of the spread price with respect to movement of value of the combined volatility σ:

.

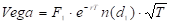Theta

Call

,

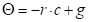Put

,

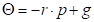where

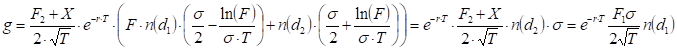
Rho

Call

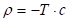
Put

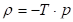
Chi

Chi 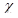(as defined in Carmona & Durrleman) denotes the first derivative of option price by correlation coefficient.

.

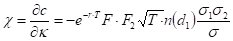Implied Volatility & Correlation

There is no definite way to calculate both σ₁, σ₂ given a concrete spot price. It is supposed to determine the value of the combined volatility σ by the standard approach of solving the equation numerically as done in Black-Scholes model.

However, it should be possible to calculate implied value of any of three σ₁, σ₂, κ variables provided the other two are known. For that purpose the partial derivatives of option value by any of three variables may be required to apply Newton’s equation solver, for instance.

Let’s denote a selected variable as ξ, which may be either of σ₁, σ₂, κ. The generic form of the partial derivative of option value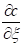is:

.

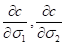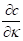The expression demonstrates that values calculated with BS model can be used. Substituting ξ with σ₁, σ₂, and κ the expressions for each of, and  can be obtained using the corresponding partial derivatives of σ given earlier.