Term
Definition
TheoV
option theoretic value
sigma, σ
volatility of the relative price change of the underlying stock price
ImpV
implied volatility
Greeks
Partial derivatives of the option price to a small movement in the underlying variables. Main Greeks are delta, gamma, theta, vega, rho.
Delta, ∆
delta is the first derivative of the option price by underlying price
Gamma, Γ
gamma is the second derivative of the option price by underlying price
Vega
vega is the first derivative of the option price by volatility
Theta, Θ
theta is the first derivative of the option price by time to expiration
Rho, ρ
rho is the first derivative of the option price by interest rate
N(x)
cumulative normal distribution function
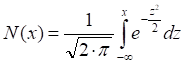
n(x)
normal distribution function
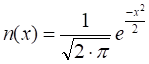 ,
, 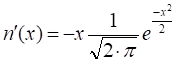
S
underlying price
X
strike price of option
r
risk-free interest rate
T
option time to expiration in years
σ
volatility of the relative price change of the underlying instrument
b
the cost-of-carry rate of holding the underlying security